一、幂函数的概念:一般地,函数【y=x^α】叫做幂函数,其中x是自变量函数,α是常数.



二、幂函数的图像与性质1、6个常见幂函数的图像与性质
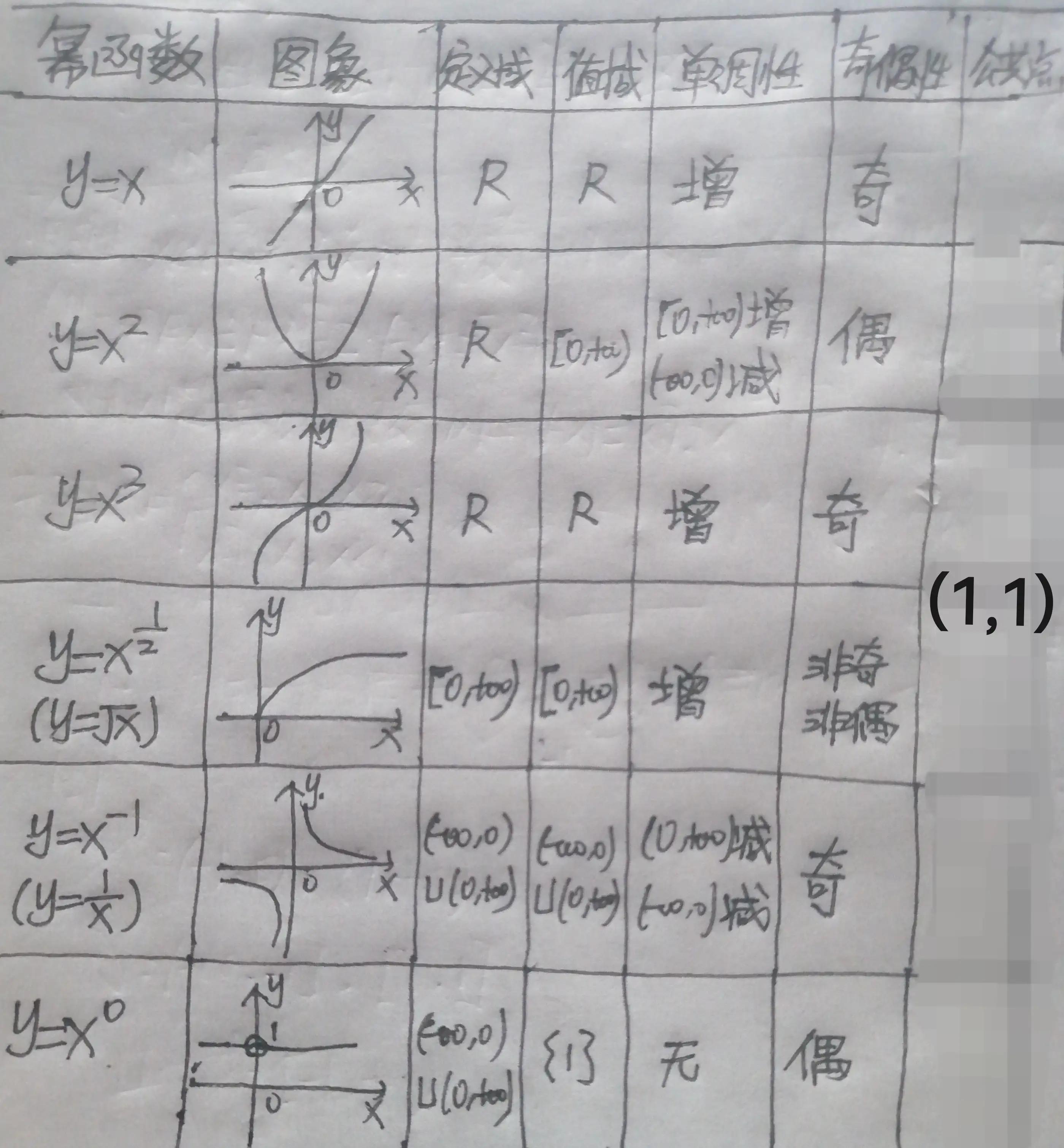
2、幂函数知识辨析
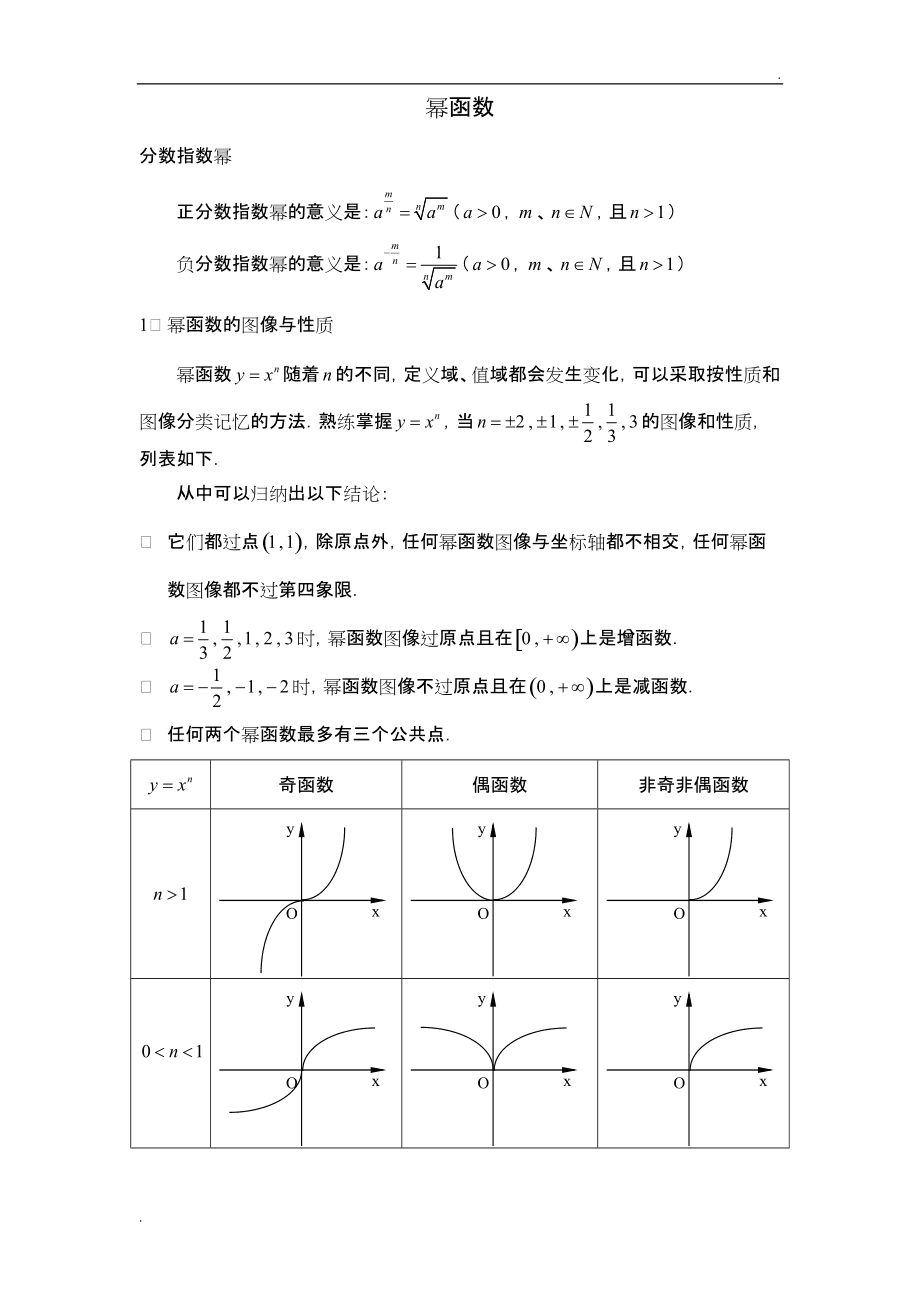
(1)幂函数的图像都过点(0,0),(1,1).【解】错,α<0时不过(0,0);
(2)幂函数的图像一定不出现在第四象限,但可能出现在第二象限.【解】对,正数的任何次幂都是正的,但复数的偶次幂是正的.
(3)当幂指数α取1,3,1/2时,幂函数y=x^α是增函数.【解】对,α>0时是增函数.
(4)当幂指数α=-1时,幂函数y=x^α在定义域上是减函数.【解】错,y=1/x在(-∞,0)和(0,+∞)上分别单调递减.
(5)当α=0时,幂函数y=x^α的图像是一条直线.【解】错,y=x^0中x≠0,故图像应该是直线y=1去除点(0,1).
(6)若幂函数y=x^α的图像关于原点对称,则在定义域内y随x的增大而增大.【解】错,y=x^α是奇函数函数,但α<0时,函数在在(-∞,0)和(0,+∞)上分别单调.
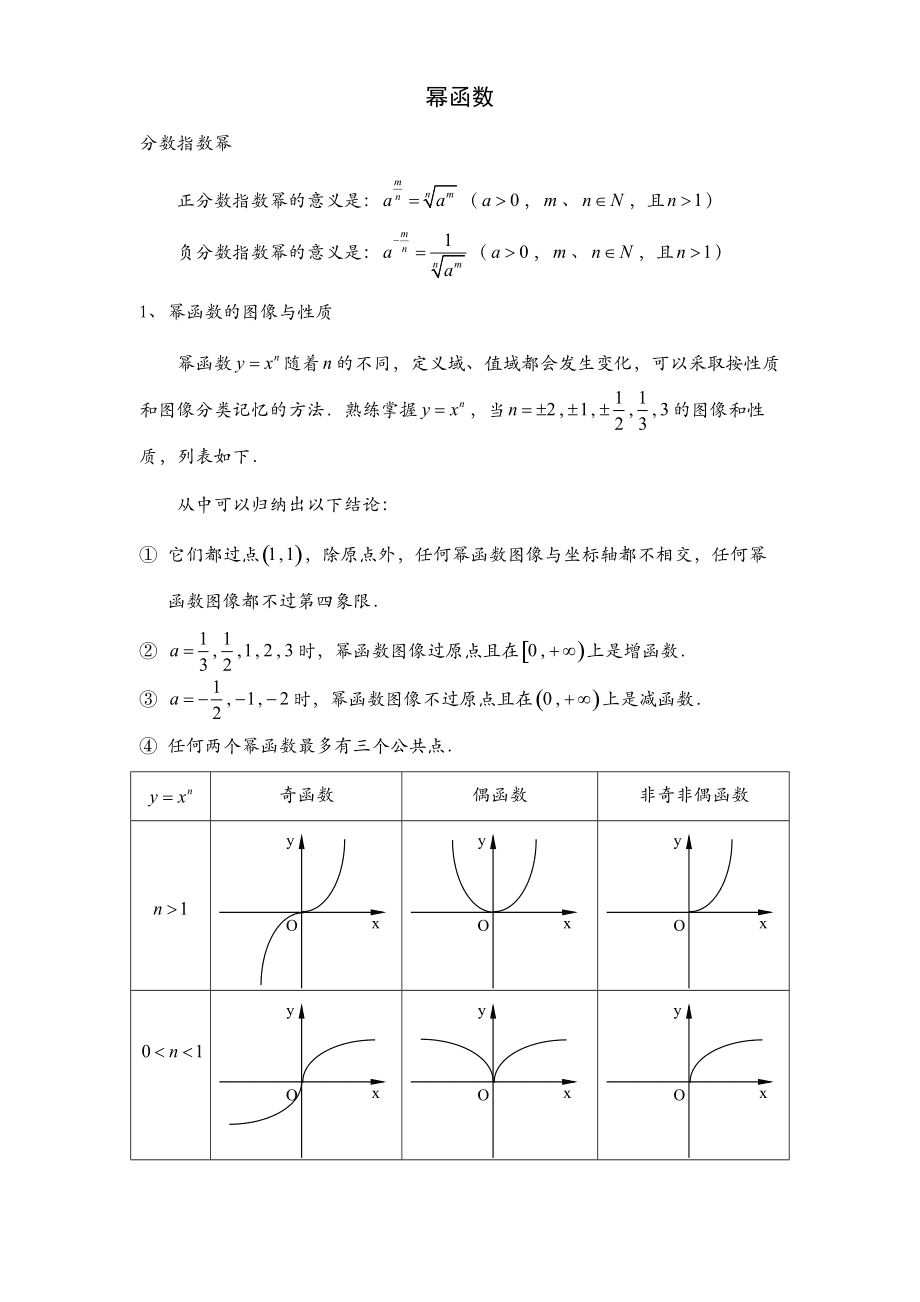
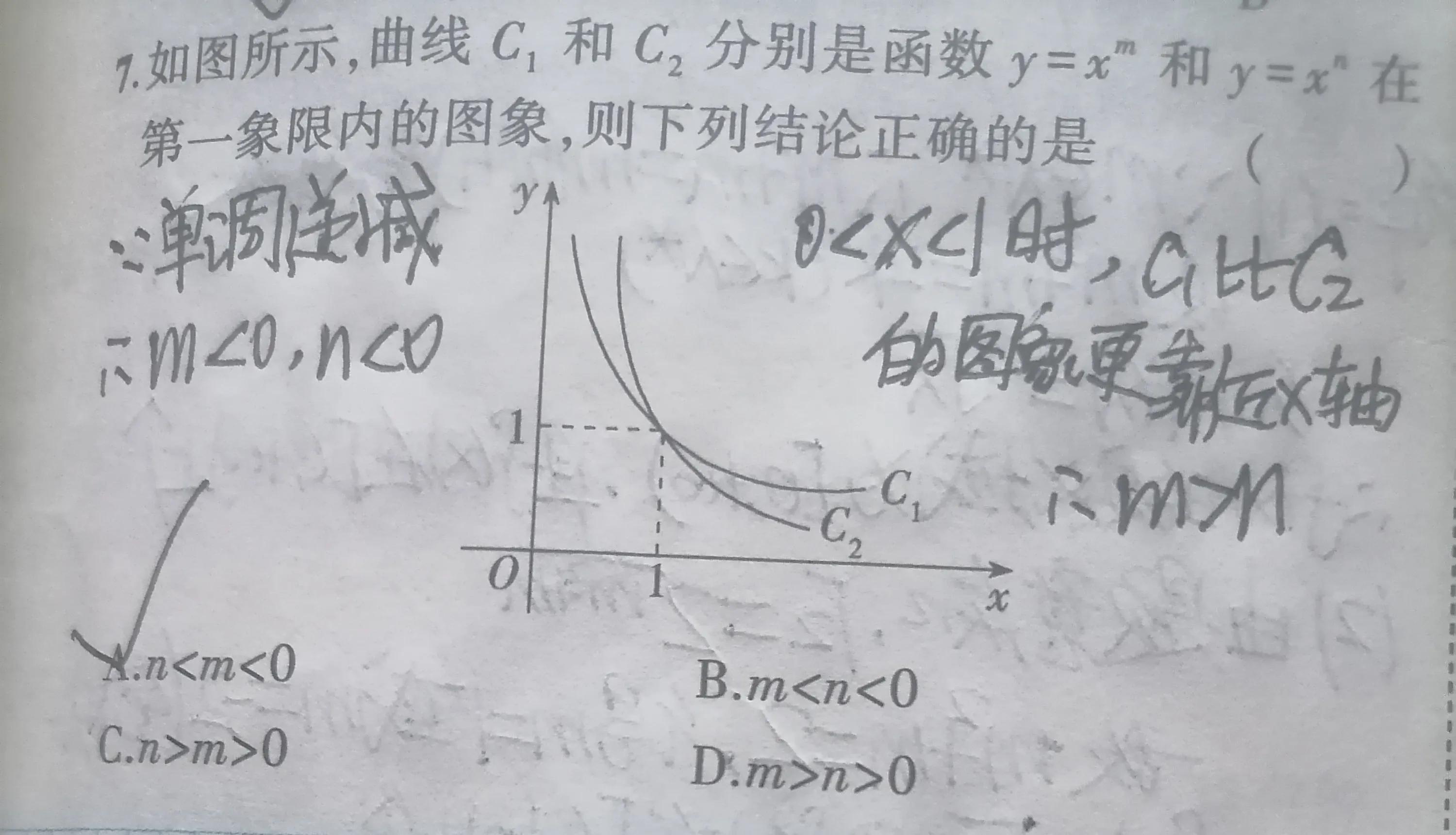
3、已知几个幂函数在同一坐标系中的位置,如何判断它们的指数大小.
根据幂函数在第一象限内的图像确定幂指数α的大小关系,结论如下:
①在(0,1)上,指数越大,图像越靠近x轴(简记为“值大图低”);
②在(1,+∞)上,指数越大,图像越远离x轴(简记为“值大图高).

三、幂函数性质的应用.
幂函数的性质与参数α可以互相确定:
(1)幂函数y=x^α中只含有一个参数α,幂函数的所有性质都与α的取值有关,故可由α确定幂函数的定义域、值域、单调性、奇偶性等.
(2)也可由幂函数的性质来得出α的值或范围:①利用单调性求出α的取值范围;②利用奇偶性结合其他条件确定α的值.




———END———
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: wxii2p22






