目录
堆排序
十大经典排序算法江山图
十大经典排序算法江山图
堆排序在排序复杂性的研究中有着重要的地位,因为他是我们所知的唯一能够同时最优的利用空间和时间的方法,当空间十分紧张的时候(例如嵌入式系统或者低成本的移动设备中)他很流行,因为他只用几行就能实现较好的性能。但是现代操作系统中很少使用他,因为他无法利用缓存,这一点很致命。数组元素很少和相邻的其他元素进行比较,因此缓存未命中的次数要远远高于大多数比较都在相邻元素间的算法,如快速排序,归并排序,甚至是希尔排序。
什么是堆?定义❝
堆(英语:Heap)是计算机科学中的一种特别的完全二叉树,满足特性”给定堆中任意节点P和C,若P是C的母节点,那么P的值会小于等于(或大于等于)C的值”。摘自维基百科。
❞
首先堆是一个完全二叉树(除了最后一层,其他层的节点个数都是满的,最后一层的节点都靠左排列),这点很重要,直接决定了数组下标和左右父节点的对应关系(关系往下看)。
分类
最小堆(min heap):母节点的值恒小于等于子节点的值;
最大堆(max heap):母节点的值恒大于等于子节点的值;
堆
值得注意,这个地方对哦左右子节点的大小没有要求。
而且,堆一般用数组来存储,而不是树。因为树需要为其左右子节点分配指针空间,而数组使用数组下标来表示左右子节点的位置堆排序,可以说堆是被树耽误了的数组,顶着树的光环成功劝退了一大批想学的人,结果实际上干着数组该干的事儿堆排序,算法史上最大的骗局,挂羊肉卖狗肉。
父节点和左右子节点在数组中的位置关系:
parent(i) = arr((i - 1)/2)
left(i) = 2i + 1
right(i) = 2i + 2
作用
构建优先队列
堆排序
找最值
你猜,面试官考你这个啥心态
值得注意,搜索不是堆的目的,并不是每一个最小(大)堆都是一个有序数组!要将堆转换成有序数组,需要使用堆排序,此处欢迎我们的堆排序隆重登场。
堆排序
正因为堆只是父子之间大小关系确定,左右子节点直接大小不确定,所以才要堆排序将所有的元素有序排序。
算法描述
以构建大顶堆为例:

将待排序序列构成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点;
将其与末尾元素进行交换,此时末尾就是最大值;
然后将剩余n-1个元素重新构造成一个大顶堆,就会得到n个元素的次大值;
反复执行前面2,3步,便能得到一个有序序列
动图演示
堆排序
图解堆排序
根据数组构造大顶堆:
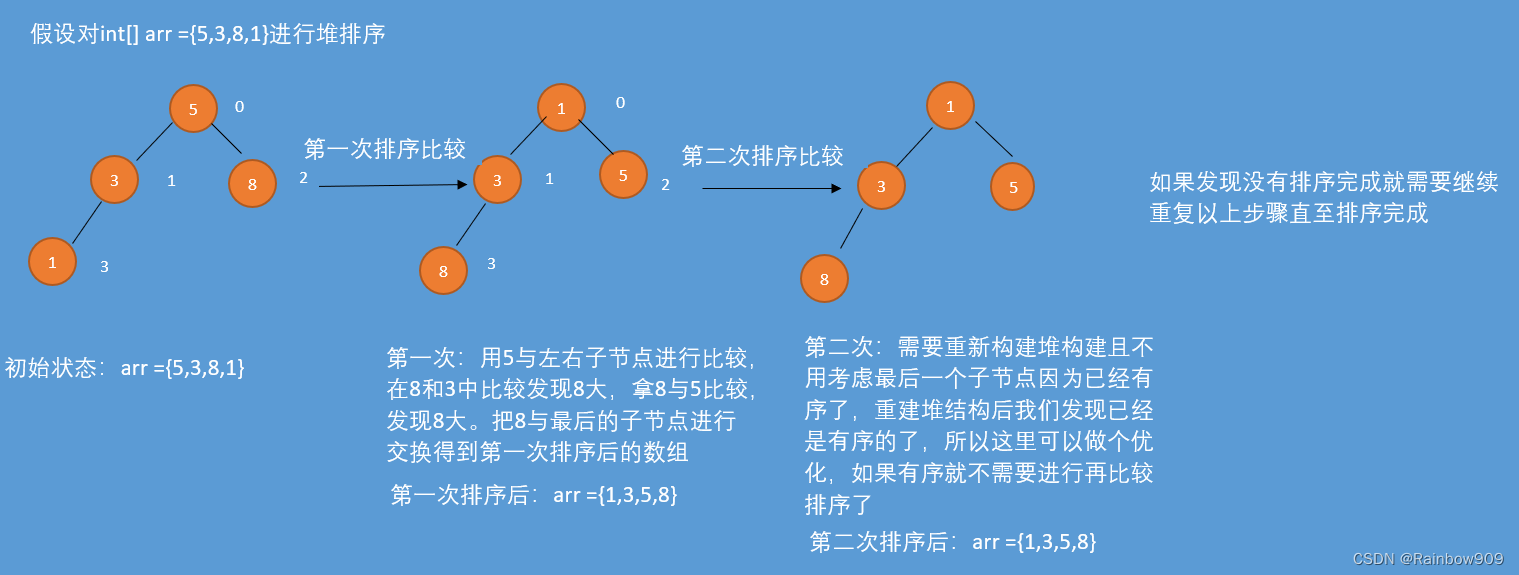
初始数组为:[6,1,2,3,0,4,5,7]
按照完全二叉树,将数字依次填入,得到图中第一幅图;
从最下面的非叶子结点开始(非叶子结点为 arr.length/2-1 = 8/2-1 =3,父节点是arr[0],arr[3]也就是3)调整,根据性质,左右子节点中小的数字往上移动;
从下至上,从右往左,递归,直到根节点
构造大顶堆
一次调整之后7成功上位,得到数组最大的值7,与此同时数组对应的大顶堆构造完成。
由下至上的堆有序化
交换调整
这里可以看到,交换调整之后最大的元素到了最下面,最终会是越下面的数越大,因此构造大顶堆得到的是降序,升序要构造小顶堆。
代码实现
import com.sun.tools.javac.util.ArrayUtils;
/**
* @author by zengzhiqin
* 2020-12-10
*/
public class HeapSort {
public static int[] heapSort (int[] arr) {
if (arr == null && arr.length == 0) {
throw new RuntimeException("数组不合法");
}
// 构建堆(从最下面叶子结点层的上一层,即倒数第二层的第一个开始进行构建调整)
for (int i = arr.length / 2 -1; i >= 0; i--) {
adjustDown(arr, i, arr.length);
}
// 循环调整下沉
for (int i = arr.length -1; i >= 0; i--) {
swap(arr, 0, i);
adjustDown(arr, 0, i);
}
return arr;
}
/**
* 调整
* @param arr
* @param parent
* @param length
*/
public static void adjustDown (int[] arr, int parent, int length) {
// 临时元素保存要下沉的元素
int temp = arr[parent];
// 左节点的位置
int leftChild = 2 * parent + 1;
// 开始往下调整
while (leftChild < length) {
// 如果右孩子节点比左孩子大,则定位到右孩子 (父节点只是比左右孩子都大,左右孩子大小不确定)
if(leftChild + 1 < length && arr[leftChild] < arr[leftChild + 1]) {
// 此时leftChild实际上是右孩子,但始终是左右里面最大的
leftChild ++ ;
}
// 大顶堆条件被破坏了
if (arr[leftChild] <= temp) {
break;
}
// 把子节点中大的值赋值给父节点
arr[parent] = arr[leftChild];
// 大的子节点为父节点,调整它的左右子节点
parent = leftChild;
leftChild = 2 * parent + 1;
}
arr[parent] = temp;
}
/**
* 交换数组中两个元素
* @param arr 数组
* @param i 父元素
* @param index 元素2
*/
public static void swap (int[] arr, int i, int index) {
int temp = arr[i];
arr[i] = arr[index];
arr[index] = temp;
}
public static void main(String[] args) {
//int[] arr = {5, 7, 8, 3, 1, 2, 4, 6, 8};
int[] arr = {3, 1, 2, 4};
//int[] arr = {1, 2, 3};
arr = heapSort(arr);
for (int i=0; i<arr.length; i++) {
System.out.println(arr[i]);
}
}
}
稳定性分析
不稳定。
时间复杂度分析
nlog(n)。
大顶堆构造使用 O(N) 的时间,元素调整下滤需要 O(logN),需要下滤 N-1 次,所以总共需要 O(N+(N-1)logN) = O(NlogN)。从过程可以看出,堆排序,不管最好,最坏时间复杂度都稳定在O(NlogN)。
空间复杂度分析
原地排序,空间复杂度O(1)
参考资料:极客时间算法训练营笔记,算法书籍






